teaching via problem solving

Center for Teaching

Teaching problem solving.

Print Version

Tips and Techniques

Expert vs. novice problem solvers, communicate.

• Have students  identify specific problems, difficulties, or confusions . Don’t waste time working through problems that students already understand.
• If students are unable to articulate their concerns, determine where they are having trouble by  asking them to identify the specific concepts or principles associated with the problem.
• In a one-on-one tutoring session, ask the student to  work his/her problem out loud . This slows down the thinking process, making it more accurate and allowing you to access understanding.
• When working with larger groups you can ask students to provide a written “two-column solution.” Have students write up their solution to a problem by putting all their calculations in one column and all of their reasoning (in complete sentences) in the other column. This helps them to think critically about their own problem solving and helps you to more easily identify where they may be having problems. Two-Column Solution (Math) Two-Column Solution (Physics)

Encourage Independence

• Model the problem solving process rather than just giving students the answer. As you work through the problem, consider how a novice might struggle with the concepts and make your thinking clear
• Have students work through problems on their own. Ask directing questions or give helpful suggestions, but  provide only minimal assistance and only when needed to overcome obstacles.
• Don’t fear  group work ! Students can frequently help each other, and talking about a problem helps them think more critically about the steps needed to solve the problem. Additionally, group work helps students realize that problems often have multiple solution strategies, some that might be more effective than others

Be sensitive

• Frequently, when working problems, students are unsure of themselves. This lack of confidence may hamper their learning. It is important to recognize this when students come to us for help, and to give each student some feeling of mastery. Do this by providing  positive reinforcement to let students know when they have mastered a new concept or skill.

Encourage Thoroughness and Patience

• Try to communicate that  the process is more important than the answer so that the student learns that it is OK to not have an instant solution. This is learned through your acceptance of his/her pace of doing things, through your refusal to let anxiety pressure you into giving the right answer, and through your example of problem solving through a step-by step process.

Experts (teachers) in a particular field are often so fluent in solving problems from that field that they can find it difficult to articulate the problem solving principles and strategies they use to novices (students) in their field because these principles and strategies are second nature to the expert. To teach students problem solving skills,  a teacher should be aware of principles and strategies of good problem solving in his or her discipline .

The mathematician George Polya captured the problem solving principles and strategies he used in his discipline in the book  How to Solve It: A New Aspect of Mathematical Method (Princeton University Press, 1957). The book includes  a summary of Polya’s problem solving heuristic as well as advice on the teaching of problem solving.

Teaching Guides

Quick Links

• Services for Departments and Schools
• Examples of Online Instructional Modules

Teaching problem solving: Let students get ‘stuck’ and ‘unstuck’

Subscribe to the center for universal education bulletin, kate mills and km kate mills literacy interventionist - red bank primary school helyn kim helyn kim former brookings expert.

October 31, 2017

This is the second in a six-part  blog series  on  teaching 21st century skills , including  problem solving ,  metacognition , critical thinking , and collaboration , in classrooms.

In the real world, students encounter problems that are complex, not well defined, and lack a clear solution and approach. They need to be able to identify and apply different strategies to solve these problems. However, problem solving skills do not necessarily develop naturally; they need to be explicitly taught in a way that can be transferred across multiple settings and contexts.

Here’s what Kate Mills, who taught 4 th grade for 10 years at Knollwood School in New Jersey and is now a Literacy Interventionist at Red Bank Primary School, has to say about creating a classroom culture of problem solvers:

Helping my students grow to be people who will be successful outside of the classroom is equally as important as teaching the curriculum. From the first day of school, I intentionally choose language and activities that help to create a classroom culture of problem solvers. I want to produce students who are able to think about achieving a particular goal and manage their mental processes . This is known as metacognition , and research shows that metacognitive skills help students become better problem solvers.

I begin by “normalizing trouble” in the classroom. Peter H. Johnston teaches the importance of normalizing struggle , of naming it, acknowledging it, and calling it what it is: a sign that we’re growing. The goal is for the students to accept challenge and failure as a chance to grow and do better.

I look for every chance to share problems and highlight how the students— not the teachers— worked through those problems. There is, of course, coaching along the way. For example, a science class that is arguing over whose turn it is to build a vehicle will most likely need a teacher to help them find a way to the balance the work in an equitable way. Afterwards, I make it a point to turn it back to the class and say, “Do you see how you …” By naming what it is they did to solve the problem , students can be more independent and productive as they apply and adapt their thinking when engaging in future complex tasks.

After a few weeks, most of the class understands that the teachers aren’t there to solve problems for the students, but to support them in solving the problems themselves. With that important part of our classroom culture established, we can move to focusing on the strategies that students might need.

Here’s one way I do this in the classroom:

I show the broken escalator video to the class. Since my students are fourth graders, they think it’s hilarious and immediately start exclaiming, “Just get off! Walk!”

When the video is over, I say, “Many of us, probably all of us, are like the man in the video yelling for help when we get stuck. When we get stuck, we stop and immediately say ‘Help!’ instead of embracing the challenge and trying new ways to work through it.” I often introduce this lesson during math class, but it can apply to any area of our lives, and I can refer to the experience and conversation we had during any part of our day.

Research shows that just because students know the strategies does not mean they will engage in the appropriate strategies. Therefore, I try to provide opportunities where students can explicitly practice learning how, when, and why to use which strategies effectively  so that they can become self-directed learners.

For example, I give students a math problem that will make many of them feel “stuck”. I will say, “Your job is to get yourselves stuck—or to allow yourselves to get stuck on this problem—and then work through it, being mindful of how you’re getting yourselves unstuck.” As students work, I check-in to help them name their process: “How did you get yourself unstuck?” or “What was your first step? What are you doing now? What might you try next?” As students talk about their process, I’ll add to a list of strategies that students are using and, if they are struggling, help students name a specific process. For instance, if a student says he wrote the information from the math problem down and points to a chart, I will say: “Oh that’s interesting. You pulled the important information from the problem out and organized it into a chart.” In this way, I am giving him the language to match what he did, so that he now has a strategy he could use in other times of struggle.

The charts grow with us over time and are something that we refer to when students are stuck or struggling. They become a resource for students and a way for them to talk about their process when they are reflecting on and monitoring what did or did not work.

For me, as a teacher, it is important that I create a classroom environment in which students are problem solvers. This helps tie struggles to strategies so that the students will not only see value in working harder but in working smarter by trying new and different strategies and revising their process. In doing so, they will more successful the next time around.

Related Content

Esther Care, Helyn Kim, Alvin Vista

October 17, 2017

David Owen, Alvin Vista

November 15, 2017

Loren Clarke, Esther Care

December 5, 2017

Global Education K-12 Education

Global Economy and Development

Center for Universal Education

Sweta Shah, Kathy Hirsh-Pasek

November 8, 2024

The Brookings Institution, Washington DC

Monday, 12:00 pm - 1:30 pm EST

Jon Valant, Katharine Meyer, Michael Hansen

November 5, 2024

• Faculty & Staff

Teaching problem solving

Strategies for teaching problem solving apply across disciplines and instructional contexts. First, introduce the problem and explain how people in your discipline generally make sense of the given information. Then, explain how to apply these approaches to solve the problem.

Introducing the problem

Explaining how people in your discipline understand and interpret these types of problems can help students develop the skills they need to understand the problem (and find a solution). After introducing how you would go about solving a problem, you could then ask students to:

• frame the problem in their own words
• define key terms and concepts
• determine statements that accurately represent the givens of a problem
• identify analogous problems
• determine what information is needed to solve the problem

Working on solutions

In the solution phase, one develops and then implements a coherent plan for solving the problem. As you help students with this phase, you might ask them to:

• identify the general model or procedure they have in mind for solving the problem
• set sub-goals for solving the problem
• identify necessary operations and steps
• draw conclusions
• carry out necessary operations

You can help students tackle a problem effectively by asking them to:

• systematically explain each step and its rationale
• explain how they would approach solving the problem
• help you solve the problem by posing questions at key points in the process
• work together in small groups (3 to 5 students) to solve the problem and then have the solution presented to the rest of the class (either by you or by a student in the group)

In all cases, the more you get the students to articulate their own understandings of the problem and potential solutions, the more you can help them develop their expertise in approaching problems in your discipline.

Why Every Educator Needs to Teach Problem-Solving Skills

Strong problem-solving skills will help students be more resilient and will increase their academic and career success .

Want to learn more about how to measure and teach students’ higher-order skills, including problem solving, critical thinking, and written communication?

Problem-solving skills are essential in school, careers, and life.

Problem-solving skills are important for every student to master. They help individuals navigate everyday life and find solutions to complex issues and challenges. These skills are especially valuable in the workplace, where employees are often required to solve problems and make decisions quickly and effectively.

Problem-solving skills are also needed for students’ personal growth and development because they help individuals overcome obstacles and achieve their goals. By developing strong problem-solving skills, students can improve their overall quality of life and become more successful in their personal and professional endeavors.

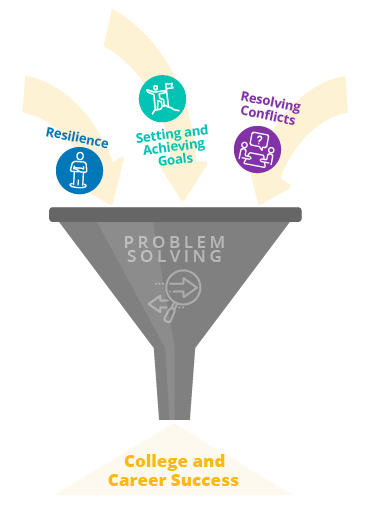
Problem-Solving Skills Help Students…

   develop resilience.

Problem-solving skills are an integral part of resilience and the ability to persevere through challenges and adversity. To effectively work through and solve a problem, students must be able to think critically and creatively. Critical and creative thinking help students approach a problem objectively, analyze its components, and determine different ways to go about finding a solution.  

This process in turn helps students build self-efficacy . When students are able to analyze and solve a problem, this increases their confidence, and they begin to realize the power they have to advocate for themselves and make meaningful change.

When students gain confidence in their ability to work through problems and attain their goals, they also begin to build a growth mindset . According to leading resilience researcher, Carol Dweck, “in a growth mindset, people believe that their most basic abilities can be developed through dedication and hard work—brains and talent are just the starting point. This view creates a love of learning and a resilience that is essential for great accomplishment.”

    Set and Achieve Goals

Students who possess strong problem-solving skills are better equipped to set and achieve their goals. By learning how to identify problems, think critically, and develop solutions, students can become more self-sufficient and confident in their ability to achieve their goals. Additionally, problem-solving skills are used in virtually all fields, disciplines, and career paths, which makes them important for everyone. Building strong problem-solving skills will help students enhance their academic and career performance and become more competitive as they begin to seek full-time employment after graduation or pursue additional education and training.

  Resolve Conflicts

In addition to increased social and emotional skills like self-efficacy and goal-setting, problem-solving skills teach students how to cooperate with others and work through disagreements and conflicts. Problem-solving promotes “thinking outside the box” and approaching a conflict by searching for different solutions. This is a very different (and more effective!) method than a more stagnant approach that focuses on placing blame or getting stuck on elements of a situation that can’t be changed.

While it’s natural to get frustrated or feel stuck when working through a conflict, students with strong problem-solving skills will be able to work through these obstacles, think more rationally, and address the situation with a more solution-oriented approach. These skills will be valuable for students in school, their careers, and throughout their lives.

    Achieve Success

We are all faced with problems every day. Problems arise in our personal lives, in school and in our jobs, and in our interactions with others. Employers especially are looking for candidates with strong problem-solving skills. In today’s job market, most jobs require the ability to analyze and effectively resolve complex issues. Students with strong problem-solving skills will stand out from other applicants and will have a more desirable skill set.

In a recent opinion piece published by The Hechinger Report , Virgel Hammonds, Chief Learning Officer at KnowledgeWorks, stated “Our world presents increasingly complex challenges. Education must adapt so that it nurtures problem solvers and critical thinkers.” Yet, the “traditional K–12 education system leaves little room for students to engage in real-world problem-solving scenarios.” This is the reason that a growing number of K–12 school districts and higher education institutions are transforming their instructional approach to personalized and competency-based learning, which encourage students to make decisions, problem solve and think critically as they take ownership of and direct their educational journey.

Problem-Solving Skills Can Be Measured and Taught

Research shows that problem-solving skills can be measured and taught. One effective method is through performance-based assessments which require students to demonstrate or apply their knowledge and higher-order skills to create a response or product or do a task.

What Are Performance-Based Assessments?

With the No Child Left Behind Act (2002), the use of standardized testing became the primary way to measure student learning in the U.S. The legislative requirements of this act shifted the emphasis to standardized testing, and this led to a  decline in nontraditional testing methods .

But   many educators, policy makers, and parents have concerns with standardized tests. Some of the top issues include that they don’t provide feedback on how students can perform better, they don’t value creativity, they are not representative of diverse populations, and they can be disadvantageous to lower-income students.

While standardized tests are still the norm, U.S. Secretary of Education Miguel Cardona is encouraging states and districts to move away from traditional multiple choice and short response tests and instead use performance-based assessment, competency-based assessments, and other more authentic methods of measuring students abilities and skills rather than rote learning. 

Performance-based assessments  measure whether students can apply the skills and knowledge learned from a unit of study. Typically, a performance task challenges students to use their higher-order skills to complete a project or process. Tasks can range from an essay to a complex proposal or design.

Preview a Performance-Based Assessment

Want a closer look at how performance-based assessments work?  Preview CAE’s K–12 and Higher Education assessments and see how CAE’s tools help students develop critical thinking, problem-solving, and written communication skills.

Performance-Based Assessments Help Students Build and Practice Problem-Solving Skills

In addition to effectively measuring students’ higher-order skills, including their problem-solving skills, performance-based assessments can help students practice and build these skills. Through the assessment process, students are given opportunities to practically apply their knowledge in real-world situations. By demonstrating their understanding of a topic, students are required to put what they’ve learned into practice through activities such as presentations, experiments, and simulations. 

This type of problem-solving assessment tool requires students to analyze information and choose how to approach the presented problems. This process enhances their critical thinking skills and creativity, as well as their problem-solving skills. Unlike traditional assessments based on memorization or reciting facts, performance-based assessments focus on the students’ decisions and solutions, and through these tasks students learn to bridge the gap between theory and practice.

Performance-based assessments like CAE’s College and Career Readiness Assessment (CRA+) and Collegiate Learning Assessment (CLA+) provide students with in-depth reports that show them which higher-order skills they are strongest in and which they should continue to develop. This feedback helps students and their teachers plan instruction and supports to deepen their learning and improve their mastery of critical skills.

Explore CAE’s Problem-Solving Assessments

CAE offers performance-based assessments that measure student proficiency in higher-order skills including problem solving, critical thinking, and written communication.

• College and Career Readiness Assessment (CCRA+) for secondary education and
• Collegiate Learning Assessment (CLA+) for higher education.

Our solution also includes instructional materials, practice models, and professional development.

We can help you create a program to build students’ problem-solving skills that includes:

• Measuring students’ problem-solving skills through a performance-based assessment    
• Using the problem-solving assessment data to inform instruction and tailor interventions
• Teaching students problem-solving skills and providing practice opportunities in real-life scenarios
• Supporting educators with quality professional development

Get started with our problem-solving assessment tools to measure and build students’ problem-solving skills today! These skills will be invaluable to students now and in the future.

Ready to Get Started?

Learn more about cae’s suite of products and let’s get started measuring and teaching students important higher-order skills like problem solving..

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

5 Teaching Mathematics Through Problem Solving

Janet Stramel

In his book “How to Solve It,” George Pólya (1945) said, “One of the most important tasks of the teacher is to help his students. This task is not quite easy; it demands time, practice, devotion, and sound principles. The student should acquire as much experience of independent work as possible. But if he is left alone with his problem without any help, he may make no progress at all. If the teacher helps too much, nothing is left to the student. The teacher should help, but not too much and not too little, so that the student shall have a reasonable share of the work.” (page 1)

What is a problem  in mathematics? A problem is “any task or activity for which the students have no prescribed or memorized rules or methods, nor is there a perception by students that there is a specific ‘correct’ solution method” (Hiebert, et. al., 1997). Problem solving in mathematics is one of the most important topics to teach; learning to problem solve helps students develop a sense of solving real-life problems and apply mathematics to real world situations. It is also used for a deeper understanding of mathematical concepts. Learning “math facts” is not enough; students must also learn how to use these facts to develop their thinking skills.

According to NCTM (2010), the term “problem solving” refers to mathematical tasks that have the potential to provide intellectual challenges for enhancing students’ mathematical understanding and development. When you first hear “problem solving,” what do you think about? Story problems or word problems? Story problems may be limited to and not “problematic” enough. For example, you may ask students to find the area of a rectangle, given the length and width. This type of problem is an exercise in computation and can be completed mindlessly without understanding the concept of area. Worthwhile problems  includes problems that are truly problematic and have the potential to provide contexts for students’ mathematical development.

There are three ways to solve problems: teaching for problem solving, teaching about problem solving, and teaching through problem solving.

Teaching for problem solving begins with learning a skill. For example, students are learning how to multiply a two-digit number by a one-digit number, and the story problems you select are multiplication problems. Be sure when you are teaching for problem solving, you select or develop tasks that can promote the development of mathematical understanding.

Teaching about problem solving begins with suggested strategies to solve a problem. For example, “draw a picture,” “make a table,” etc. You may see posters in teachers’ classrooms of the “Problem Solving Method” such as: 1) Read the problem, 2) Devise a plan, 3) Solve the problem, and 4) Check your work. There is little or no evidence that students’ problem-solving abilities are improved when teaching about problem solving. Students will see a word problem as a separate endeavor and focus on the steps to follow rather than the mathematics. In addition, students will tend to use trial and error instead of focusing on sense making.

Teaching through problem solving  focuses students’ attention on ideas and sense making and develops mathematical practices. Teaching through problem solving also develops a student’s confidence and builds on their strengths. It allows for collaboration among students and engages students in their own learning.

Consider the following worthwhile-problem criteria developed by Lappan and Phillips (1998):

• The problem has important, useful mathematics embedded in it.
• The problem requires high-level thinking and problem solving.
• The problem contributes to the conceptual development of students.
• The problem creates an opportunity for the teacher to assess what his or her students are learning and where they are experiencing difficulty.
• The problem can be approached by students in multiple ways using different solution strategies.
• The problem has various solutions or allows different decisions or positions to be taken and defended.
• The problem encourages student engagement and discourse.
• The problem connects to other important mathematical ideas.
• The problem promotes the skillful use of mathematics.
• The problem provides an opportunity to practice important skills.

Of course, not every problem will include all of the above. Sometimes, you will choose a problem because your students need an opportunity to practice a certain skill.

Key features of a good mathematics problem includes:

• It must begin where the students are mathematically.
• The feature of the problem must be the mathematics that students are to learn.
• It must require justifications and explanations for both answers and methods of solving.

Problem solving is not a  neat and orderly process. Think about needlework. On the front side, it is neat and perfect and pretty.

But look at the b ack.

It is messy and full of knots and loops. Problem solving in mathematics is also like this and we need to help our students be “messy” with problem solving; they need to go through those knots and loops and learn how to solve problems with the teacher’s guidance.

When you teach through problem solving , your students are focused on ideas and sense-making and they develop confidence in mathematics!

Mathematics Tasks and Activities that Promote Teaching through Problem Solving

Choosing the Right Task

Selecting activities and/or tasks is the most significant decision teachers make that will affect students’ learning. Consider the following questions:

• Teachers must do the activity first. What is problematic about the activity? What will you need to do BEFORE the activity and AFTER the activity? Additionally, think how your students would do the activity.
• What mathematical ideas will the activity develop? Are there connections to other related mathematics topics, or other content areas?
• Can the activity accomplish your learning objective/goals?

Low Floor High Ceiling Tasks

By definition, a “ low floor/high ceiling task ” is a mathematical activity where everyone in the group can begin and then work on at their own level of engagement. Low Floor High Ceiling Tasks are activities that everyone can begin and work on based on their own level, and have many possibilities for students to do more challenging mathematics. One gauge of knowing whether an activity is a Low Floor High Ceiling Task is when the work on the problems becomes more important than the answer itself, and leads to rich mathematical discourse [Hover: ways of representing, thinking, talking, agreeing, and disagreeing; the way ideas are exchanged and what the ideas entail; and as being shaped by the tasks in which students engage as well as by the nature of the learning environment].

The strengths of using Low Floor High Ceiling Tasks:

• Allows students to show what they can do, not what they can’t.
• Provides differentiation to all students.
• Promotes a positive classroom environment.
• Advances a growth mindset in students
• Aligns with the Standards for Mathematical Practice

Examples of some Low Floor High Ceiling Tasks can be found at the following sites:

• YouCubed – under grades choose Low Floor High Ceiling
• NRICH Creating a Low Threshold High Ceiling Classroom
• Inside Mathematics Problems of the Month

Math in 3-Acts

Math in 3-Acts was developed by Dan Meyer to spark an interest in and engage students in thought-provoking mathematical inquiry. Math in 3-Acts is a whole-group mathematics task consisting of three distinct parts:

Act One is about noticing and wondering. The teacher shares with students an image, video, or other situation that is engaging and perplexing. Students then generate questions about the situation.

In Act Two , the teacher offers some information for the students to use as they find the solutions to the problem.

Act Three is the “reveal.” Students share their thinking as well as their solutions.

“Math in 3 Acts” is a fun way to engage your students, there is a low entry point that gives students confidence, there are multiple paths to a solution, and it encourages students to work in groups to solve the problem. Some examples of Math in 3-Acts can be found at the following websites:

• Dan Meyer’s Three-Act Math Tasks
• Graham Fletcher3-Act Tasks ]
• Math in 3-Acts: Real World Math Problems to Make Math Contextual, Visual and Concrete

Number Talks

Number talks are brief, 5-15 minute discussions that focus on student solutions for a mental math computation problem. Students share their different mental math processes aloud while the teacher records their thinking visually on a chart or board. In addition, students learn from each other’s strategies as they question, critique, or build on the strategies that are shared.. To use a “number talk,” you would include the following steps:

• The teacher presents a problem for students to solve mentally.
• Provide adequate “ wait time .”
• The teacher calls on a students and asks, “What were you thinking?” and “Explain your thinking.”
• For each student who volunteers to share their strategy, write their thinking on the board. Make sure to accurately record their thinking; do not correct their responses.
• Invite students to question each other about their strategies, compare and contrast the strategies, and ask for clarification about strategies that are confusing.

“Number Talks” can be used as an introduction, a warm up to a lesson, or an extension. Some examples of Number Talks can be found at the following websites:

• Inside Mathematics Number Talks
• Number Talks Build Numerical Reasoning

Saying “This is Easy”

“This is easy.” Three little words that can have a big impact on students. What may be “easy” for one person, may be more “difficult” for someone else. And saying “this is easy” defeats the purpose of a growth mindset classroom, where students are comfortable making mistakes.

When the teacher says, “this is easy,” students may think,

• “Everyone else understands and I don’t. I can’t do this!”
• Students may just give up and surrender the mathematics to their classmates.
• Students may shut down.

Instead, you and your students could say the following:

• “I think I can do this.”
• “I have an idea I want to try.”
• “I’ve seen this kind of problem before.”

Tracy Zager wrote a short article, “This is easy”: The Little Phrase That Causes Big Problems” that can give you more information. Read Tracy Zager’s article here.

Using “Worksheets”

Do you want your students to memorize concepts, or do you want them to understand and apply the mathematics for different situations?

What is a “worksheet” in mathematics? It is a paper and pencil assignment when no other materials are used. A worksheet does not allow your students to use hands-on materials/manipulatives [Hover: physical objects that are used as teaching tools to engage students in the hands-on learning of mathematics]; and worksheets are many times “naked number” with no context. And a worksheet should not be used to enhance a hands-on activity.

Students need time to explore and manipulate materials in order to learn the mathematics concept. Worksheets are just a test of rote memory. Students need to develop those higher-order thinking skills, and worksheets will not allow them to do that.

One productive belief from the NCTM publication, Principles to Action (2014), states, “Students at all grade levels can benefit from the use of physical and virtual manipulative materials to provide visual models of a range of mathematical ideas.”

You may need an “activity sheet,” a “graphic organizer,” etc. as you plan your mathematics activities/lessons, but be sure to include hands-on manipulatives. Using manipulatives can

• Provide your students a bridge between the concrete and abstract
• Serve as models that support students’ thinking
• Provide another representation
• Support student engagement
• Give students ownership of their own learning.

Adapted from “ The Top 5 Reasons for Using Manipulatives in the Classroom ”.

any task or activity for which the students have no prescribed or memorized rules or methods, nor is there a perception by students that there is a specific ‘correct’ solution method

should be intriguing and contain a level of challenge that invites speculation and hard work, and directs students to investigate important mathematical ideas and ways of thinking toward the learning

involves teaching a skill so that a student can later solve a story problem

when we teach students how to problem solve

teaching mathematics content through real contexts, problems, situations, and models

a mathematical activity where everyone in the group can begin and then work on at their own level of engagement

20 seconds to 2 minutes for students to make sense of questions

Mathematics Methods for Early Childhood Copyright © 2021 by Janet Stramel is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book