CPM Educational Program
Expert textbook solutions.
Browse your textbook to find expert solutions, hints, and answers for all exercises. The solutions are always presented as a clear and concise, step-by-step explanation with included theory and helpful figures, graphs, and diagrams. Mathleaks covers the most commonly adopted textbooks with more than 250000 expert solutions.

Mathleaks Solver
With Mathleaks, you’re not tied to your textbook for solutions. Instead, scan and solve exercises with our math solver, which instantly reads the problem by using the camera on your smartphone or tablet. Access the solver through the Mathleaks app or on our website. The Mathleaks solver works for Pre-Algebra, Algebra 1, and Algebra 2.
Mathleaks Community
Get access to the world's most popular math community with Mathleaks. You can connect with other students all over the US who are studying with the same textbook or in the same math course.
Study math more efficiently using Mathleaks for CPM Educational Program textbooks.
- Core Connections Integrated I, 2013
- Core Connections Algebra 1, 2013
- Core Connections Geometry, 2013
- Core Connections Algebra 2, 2013
- Core Connections Integrated I, 2014
- Core Connections Integrated II, 2015
- Core Connections: Course 1
- Core Connections: Course 2
- Core Connections: Course 3
- Core Connections Integrated III, 2015
3.1 Functions and Function Notation
- ⓑ yes (Note: If two players had been tied for, say, 4th place, then the name would not have been a function of rank.)
w = f ( d ) w = f ( d )
g ( 5 ) = 1 g ( 5 ) = 1
m = 8 m = 8
y = f ( x ) = x 3 2 y = f ( x ) = x 3 2
g ( 1 ) = 8 g ( 1 ) = 8
x = 0 x = 0 or x = 2 x = 2
- ⓐ yes, because each bank account has a single balance at any given time;
- ⓑ no, because several bank account numbers may have the same balance;
- ⓒ no, because the same output may correspond to more than one input.
- ⓐ Yes, letter grade is a function of percent grade;
- ⓑ No, it is not one-to-one. There are 100 different percent numbers we could get but only about five possible letter grades, so there cannot be only one percent number that corresponds to each letter grade.
No, because it does not pass the horizontal line test.
3.2 Domain and Range
{ − 5 , 0 , 5 , 10 , 15 } { − 5 , 0 , 5 , 10 , 15 }
( − ∞ , ∞ ) ( − ∞ , ∞ )
( − ∞ , 1 2 ) ∪ ( 1 2 , ∞ ) ( − ∞ , 1 2 ) ∪ ( 1 2 , ∞ )
[ − 5 2 , ∞ ) [ − 5 2 , ∞ )
- ⓐ values that are less than or equal to –2, or values that are greater than or equal to –1 and less than 3
- ⓑ { x | x ≤ − 2 or − 1 ≤ x < 3 } { x | x ≤ − 2 or − 1 ≤ x < 3 }
- ⓒ ( − ∞ , − 2 ] ∪ [ − 1 , 3 ) ( − ∞ , − 2 ] ∪ [ − 1 , 3 )
domain =[1950,2002] range = [47,000,000,89,000,000]
domain: ( − ∞ , 2 ] ; ( − ∞ , 2 ] ; range: ( − ∞ , 0 ] ( − ∞ , 0 ]
3.3 Rates of Change and Behavior of Graphs
$ 2.84 − $ 2.31 5 years = $ 0.53 5 years = $ 0.106 $ 2.84 − $ 2.31 5 years = $ 0.53 5 years = $ 0.106 per year.
a + 7 a + 7
The local maximum appears to occur at ( − 1 , 28 ) , ( − 1 , 28 ) , and the local minimum occurs at ( 5 , − 80 ) . ( 5 , − 80 ) . The function is increasing on ( − ∞ , − 1 ) ∪ ( 5 , ∞ ) ( − ∞ , − 1 ) ∪ ( 5 , ∞ ) and decreasing on ( − 1 , 5 ) . ( − 1 , 5 ) .
3.4 Composition of Functions
( f g ) ( x ) = f ( x ) g ( x ) = ( x − 1 ) ( x 2 − 1 ) = x 3 − x 2 − x + 1 ( f − g ) ( x ) = f ( x ) − g ( x ) = ( x − 1 ) − ( x 2 − 1 ) = x − x 2 ( f g ) ( x ) = f ( x ) g ( x ) = ( x − 1 ) ( x 2 − 1 ) = x 3 − x 2 − x + 1 ( f − g ) ( x ) = f ( x ) − g ( x ) = ( x − 1 ) − ( x 2 − 1 ) = x − x 2
No, the functions are not the same.
A gravitational force is still a force, so a ( G ( r ) ) a ( G ( r ) ) makes sense as the acceleration of a planet at a distance r from the Sun (due to gravity), but G ( a ( F ) ) G ( a ( F ) ) does not make sense.
f ( g ( 1 ) ) = f ( 3 ) = 3 f ( g ( 1 ) ) = f ( 3 ) = 3 and g ( f ( 4 ) ) = g ( 1 ) = 3 g ( f ( 4 ) ) = g ( 1 ) = 3
g ( f ( 2 ) ) = g ( 5 ) = 3 g ( f ( 2 ) ) = g ( 5 ) = 3
[ − 4 , 0 ) ∪ ( 0 , ∞ ) [ − 4 , 0 ) ∪ ( 0 , ∞ )
Possible answer:
g ( x ) = 4 + x 2 h ( x ) = 4 3 − x f = h ∘ g g ( x ) = 4 + x 2 h ( x ) = 4 3 − x f = h ∘ g
3.5 Transformation of Functions
The graphs of f ( x ) f ( x ) and g ( x ) g ( x ) are shown below. The transformation is a horizontal shift. The function is shifted to the left by 2 units.
g ( x ) = 1 x - 1 + 1 g ( x ) = 1 x - 1 + 1
g ( x ) = − f ( x ) g ( x ) = − f ( x )
| -2 | 0 | 2 | 4 | |
h ( x ) = f ( − x ) h ( x ) = f ( − x )
| -2 | 0 | 2 | 4 | |
| 15 | 10 | 5 | unknown |
Notice: g ( x ) = f ( − x ) g ( x ) = f ( − x ) looks the same as f ( x ) f ( x ) .
| 2 | 4 | 6 | 8 | |
| 9 | 12 | 15 | 0 |
g ( x ) = 3 x - 2 g ( x ) = 3 x - 2
g ( x ) = f ( 1 3 x ) g ( x ) = f ( 1 3 x ) so using the square root function we get g ( x ) = 1 3 x g ( x ) = 1 3 x
3.6 Absolute Value Functions
using the variable p p for passing, | p − 80 | ≤ 20 | p − 80 | ≤ 20
f ( x ) = − | x + 2 | + 3 f ( x ) = − | x + 2 | + 3
x = − 1 x = − 1 or x = 2 x = 2
3.7 Inverse Functions
h ( 2 ) = 6 h ( 2 ) = 6
The domain of function f − 1 f − 1 is ( − ∞ , − 2 ) ( − ∞ , − 2 ) and the range of function f − 1 f − 1 is ( 1 , ∞ ) . ( 1 , ∞ ) .
- ⓐ f ( 60 ) = 50. f ( 60 ) = 50. In 60 minutes, 50 miles are traveled.
- ⓑ f − 1 ( 60 ) = 70. f − 1 ( 60 ) = 70. To travel 60 miles, it will take 70 minutes.
x = 3 y + 5 x = 3 y + 5
f − 1 ( x ) = ( 2 − x ) 2 ; domain of f : [ 0 , ∞ ) ; domain of f − 1 : ( − ∞ , 2 ] f − 1 ( x ) = ( 2 − x ) 2 ; domain of f : [ 0 , ∞ ) ; domain of f − 1 : ( − ∞ , 2 ]
3.1 Section Exercises
A relation is a set of ordered pairs. A function is a special kind of relation in which no two ordered pairs have the same first coordinate.
When a vertical line intersects the graph of a relation more than once, that indicates that for that input there is more than one output. At any particular input value, there can be only one output if the relation is to be a function.
When a horizontal line intersects the graph of a function more than once, that indicates that for that output there is more than one input. A function is one-to-one if each output corresponds to only one input.
not a function
f ( − 3 ) = − 11 ; f ( − 3 ) = − 11 ; f ( 2 ) = − 1 ; f ( 2 ) = − 1 ; f ( − a ) = − 2 a − 5 ; f ( − a ) = − 2 a − 5 ; − f ( a ) = − 2 a + 5 ; − f ( a ) = − 2 a + 5 ; f ( a + h ) = 2 a + 2 h − 5 f ( a + h ) = 2 a + 2 h − 5
f ( − 3 ) = 5 + 5 ; f ( − 3 ) = 5 + 5 ; f ( 2 ) = 5 ; f ( 2 ) = 5 ; f ( − a ) = 2 + a + 5 ; f ( − a ) = 2 + a + 5 ; − f ( a ) = − 2 − a − 5 ; − f ( a ) = − 2 − a − 5 ; f ( a + h ) = 2 − a − h + 5 f ( a + h ) = 2 − a − h + 5
f ( − 3 ) = 2 ; f ( − 3 ) = 2 ; f ( 2 ) = 1 − 3 = − 2 ; f ( 2 ) = 1 − 3 = − 2 ; f ( − a ) = | − a − 1 | − | − a + 1 | ; f ( − a ) = | − a − 1 | − | − a + 1 | ; − f ( a ) = − | a − 1 | + | a + 1 | ; − f ( a ) = − | a − 1 | + | a + 1 | ; f ( a + h ) = | a + h − 1 | − | a + h + 1 | f ( a + h ) = | a + h − 1 | − | a + h + 1 |
g ( x ) − g ( a ) x − a = x + a + 2 , x ≠ a g ( x ) − g ( a ) x − a = x + a + 2 , x ≠ a
a. f ( − 2 ) = 14 ; f ( − 2 ) = 14 ; b. x = 3 x = 3
a. f ( 5 ) = 10 ; f ( 5 ) = 10 ; b. x = − 1 x = − 1 or x = 4 x = 4
- ⓐ f ( t ) = 6 − 2 3 t ; f ( t ) = 6 − 2 3 t ;
- ⓑ f ( − 3 ) = 8 ; f ( − 3 ) = 8 ;
- ⓒ t = 6 t = 6
- ⓐ f ( 0 ) = 1 ; f ( 0 ) = 1 ;
- ⓑ f ( x ) = − 3 , x = − 2 f ( x ) = − 3 , x = − 2 or x = 2 x = 2
not a function so it is also not a one-to-one function
one-to- one function
function, but not one-to-one
f ( x ) = 1 , x = 2 f ( x ) = 1 , x = 2
f ( − 2 ) = 14 ; f ( − 1 ) = 11 ; f ( 0 ) = 8 ; f ( 1 ) = 5 ; f ( 2 ) = 2 f ( − 2 ) = 14 ; f ( − 1 ) = 11 ; f ( 0 ) = 8 ; f ( 1 ) = 5 ; f ( 2 ) = 2
f ( − 2 ) = 4 ; f ( − 1 ) = 4.414 ; f ( 0 ) = 4.732 ; f ( 1 ) = 5 ; f ( 2 ) = 5.236 f ( − 2 ) = 4 ; f ( − 1 ) = 4.414 ; f ( 0 ) = 4.732 ; f ( 1 ) = 5 ; f ( 2 ) = 5.236
f ( − 2 ) = 1 9 ; f ( − 1 ) = 1 3 ; f ( 0 ) = 1 ; f ( 1 ) = 3 ; f ( 2 ) = 9 f ( − 2 ) = 1 9 ; f ( − 1 ) = 1 3 ; f ( 0 ) = 1 ; f ( 1 ) = 3 ; f ( 2 ) = 9
[ 0 , 100 ] [ 0 , 100 ]
[ − 0.001 , 0 .001 ] [ − 0.001 , 0 .001 ]
[ − 1 , 000 , 000 , 1,000,000 ] [ − 1 , 000 , 000 , 1,000,000 ]
[ 0 , 10 ] [ 0 , 10 ]
[ −0.1 , 0.1 ] [ −0.1 , 0.1 ]
[ − 100 , 100 ] [ − 100 , 100 ]
- ⓐ g ( 5000 ) = 50 ; g ( 5000 ) = 50 ;
- ⓑ The number of cubic yards of dirt required for a garden of 100 square feet is 1.
- ⓐ The height of a rocket above ground after 1 second is 200 ft.
- ⓑ The height of a rocket above ground after 2 seconds is 350 ft.
3.2 Section Exercises
The domain of a function depends upon what values of the independent variable make the function undefined or imaginary.
There is no restriction on x x for f ( x ) = x 3 f ( x ) = x 3 because you can take the cube root of any real number. So the domain is all real numbers, ( − ∞ , ∞ ) . ( − ∞ , ∞ ) . When dealing with the set of real numbers, you cannot take the square root of negative numbers. So x x -values are restricted for f ( x ) = x f ( x ) = x to nonnegative numbers and the domain is [ 0 , ∞ ) . [ 0 , ∞ ) .
Graph each formula of the piecewise function over its corresponding domain. Use the same scale for the x x -axis and y y -axis for each graph. Indicate inclusive endpoints with a solid circle and exclusive endpoints with an open circle. Use an arrow to indicate − ∞ − ∞ or ∞ . ∞ . Combine the graphs to find the graph of the piecewise function.
( − ∞ , 3 ] ( − ∞ , 3 ]
( − ∞ , − 1 2 ) ∪ ( − 1 2 , ∞ ) ( − ∞ , − 1 2 ) ∪ ( − 1 2 , ∞ )
( − ∞ , − 11 ) ∪ ( − 11 , 2 ) ∪ ( 2 , ∞ ) ( − ∞ , − 11 ) ∪ ( − 11 , 2 ) ∪ ( 2 , ∞ )
( − ∞ , − 3 ) ∪ ( − 3 , 5 ) ∪ ( 5 , ∞ ) ( − ∞ , − 3 ) ∪ ( − 3 , 5 ) ∪ ( 5 , ∞ )
( − ∞ , 5 ) ( − ∞ , 5 )
[ 6 , ∞ ) [ 6 , ∞ )
( − ∞ , − 9 ) ∪ ( − 9 , 9 ) ∪ ( 9 , ∞ ) ( − ∞ , − 9 ) ∪ ( − 9 , 9 ) ∪ ( 9 , ∞ )
domain: ( 2 , 8 ] , ( 2 , 8 ] , range [ 6 , 8 ) [ 6 , 8 )
domain: [ − 4 , 4], [ − 4 , 4], range: [ 0 , 2] [ 0 , 2]
domain: [ − 5 , 3 ) , [ − 5 , 3 ) , range: [ 0 , 2 ] [ 0 , 2 ]
domain: ( − ∞ , 1 ] , ( − ∞ , 1 ] , range: [ 0 , ∞ ) [ 0 , ∞ )
domain: [ − 6 , − 1 6 ] ∪ [ 1 6 , 6 ] ; [ − 6 , − 1 6 ] ∪ [ 1 6 , 6 ] ; range: [ − 6 , − 1 6 ] ∪ [ 1 6 , 6 ] [ − 6 , − 1 6 ] ∪ [ 1 6 , 6 ]
domain: [ − 3 , ∞ ) ; [ − 3 , ∞ ) ; range: [ 0 , ∞ ) [ 0 , ∞ )
domain: ( − ∞ , ∞ ) ( − ∞ , ∞ )
f ( − 3 ) = 1 ; f ( − 2 ) = 0 ; f ( − 1 ) = 0 ; f ( 0 ) = 0 f ( − 3 ) = 1 ; f ( − 2 ) = 0 ; f ( − 1 ) = 0 ; f ( 0 ) = 0
f ( − 1 ) = − 4 ; f ( 0 ) = 6 ; f ( 2 ) = 20 ; f ( 4 ) = 34 f ( − 1 ) = − 4 ; f ( 0 ) = 6 ; f ( 2 ) = 20 ; f ( 4 ) = 34
f ( − 1 ) = − 5 ; f ( 0 ) = 3 ; f ( 2 ) = 3 ; f ( 4 ) = 16 f ( − 1 ) = − 5 ; f ( 0 ) = 3 ; f ( 2 ) = 3 ; f ( 4 ) = 16
domain: ( − ∞ , 1 ) ∪ ( 1 , ∞ ) ( − ∞ , 1 ) ∪ ( 1 , ∞ )
window: [ − 0.5 , − 0.1 ] ; [ − 0.5 , − 0.1 ] ; range: [ 4 , 100 ] [ 4 , 100 ]
window: [ 0.1 , 0.5 ] ; [ 0.1 , 0.5 ] ; range: [ 4 , 100 ] [ 4 , 100 ]
[ 0 , 8 ] [ 0 , 8 ]
Many answers. One function is f ( x ) = 1 x − 2 . f ( x ) = 1 x − 2 .
- ⓐ The fixed cost is $500.
- ⓑ The cost of making 25 items is $750.
- ⓒ The domain is [0, 100] and the range is [500, 1500].
3.3 Section Exercises
Yes, the average rate of change of all linear functions is constant.
The absolute maximum and minimum relate to the entire graph, whereas the local extrema relate only to a specific region around an open interval.
4 ( b + 1 ) 4 ( b + 1 )
4 x + 2 h 4 x + 2 h
− 1 13 ( 13 + h ) − 1 13 ( 13 + h )
3 h 2 + 9 h + 9 3 h 2 + 9 h + 9
4 x + 2 h − 3 4 x + 2 h − 3
increasing on ( − ∞ , − 2.5 ) ∪ ( 1 , ∞ ) , ( − ∞ , − 2.5 ) ∪ ( 1 , ∞ ) , decreasing on ( − 2.5 , 1 ) ( − 2.5 , 1 )
increasing on ( − ∞ , 1 ) ∪ ( 3 , 4 ) , ( − ∞ , 1 ) ∪ ( 3 , 4 ) , decreasing on ( 1 , 3 ) ∪ ( 4 , ∞ ) ( 1 , 3 ) ∪ ( 4 , ∞ )
local maximum: ( − 3 , 60 ) , ( − 3 , 60 ) , local minimum: ( 3 , − 60 ) ( 3 , − 60 )
absolute maximum at approximately ( 7 , 150 ) , ( 7 , 150 ) , absolute minimum at approximately ( −7.5 , −220 ) ( −7.5 , −220 )
Local minimum at ( 3 , − 22 ) , ( 3 , − 22 ) , decreasing on ( − ∞ , 3 ) , ( − ∞ , 3 ) , increasing on ( 3 , ∞ ) ( 3 , ∞ )
Local minimum at ( − 2 , − 2 ) , ( − 2 , − 2 ) , decreasing on ( − 3 , − 2 ) , ( − 3 , − 2 ) , increasing on ( − 2 , ∞ ) ( − 2 , ∞ )
Local maximum at ( − 0.5 , 6 ) , ( − 0.5 , 6 ) , local minima at ( − 3.25 , − 47 ) ( − 3.25 , − 47 ) and ( 2.1 , − 32 ) , ( 2.1 , − 32 ) , decreasing on ( − ∞ , − 3.25 ) ( − ∞ , − 3.25 ) and ( − 0.5 , 2.1 ) , ( − 0.5 , 2.1 ) , increasing on ( − 3.25 , − 0.5 ) ( − 3.25 , − 0.5 ) and ( 2.1 , ∞ ) ( 2.1 , ∞ )
b = 5 b = 5
2.7 gallons per minute
approximately –0.6 milligrams per day
3.4 Section Exercises
Find the numbers that make the function in the denominator g g equal to zero, and check for any other domain restrictions on f f and g , g , such as an even-indexed root or zeros in the denominator.
Yes. Sample answer: Let f ( x ) = x + 1 and g ( x ) = x − 1. f ( x ) = x + 1 and g ( x ) = x − 1. Then f ( g ( x ) ) = f ( x − 1 ) = ( x − 1 ) + 1 = x f ( g ( x ) ) = f ( x − 1 ) = ( x − 1 ) + 1 = x and g ( f ( x ) ) = g ( x + 1 ) = ( x + 1 ) − 1 = x . g ( f ( x ) ) = g ( x + 1 ) = ( x + 1 ) − 1 = x . So f ∘ g = g ∘ f . f ∘ g = g ∘ f .
( f + g ) ( x ) = 2 x + 6 , ( f + g ) ( x ) = 2 x + 6 , domain: ( − ∞ , ∞ ) ( − ∞ , ∞ )
( f − g ) ( x ) = 2 x 2 + 2 x − 6 , ( f − g ) ( x ) = 2 x 2 + 2 x − 6 , domain: ( − ∞ , ∞ ) ( − ∞ , ∞ )
( f g ) ( x ) = − x 4 − 2 x 3 + 6 x 2 + 12 x , ( f g ) ( x ) = − x 4 − 2 x 3 + 6 x 2 + 12 x , domain: ( − ∞ , ∞ ) ( − ∞ , ∞ )
( f g ) ( x ) = x 2 + 2 x 6 − x 2 , ( f g ) ( x ) = x 2 + 2 x 6 − x 2 , domain: ( − ∞ , − 6 ) ∪ ( − 6 , 6 ) ∪ ( 6 , ∞ ) ( − ∞ , − 6 ) ∪ ( − 6 , 6 ) ∪ ( 6 , ∞ )
( f + g ) ( x ) = 4 x 3 + 8 x 2 + 1 2 x , ( f + g ) ( x ) = 4 x 3 + 8 x 2 + 1 2 x , domain: ( − ∞ , 0 ) ∪ ( 0 , ∞ ) ( − ∞ , 0 ) ∪ ( 0 , ∞ )
( f − g ) ( x ) = 4 x 3 + 8 x 2 − 1 2 x , ( f − g ) ( x ) = 4 x 3 + 8 x 2 − 1 2 x , domain: ( − ∞ , 0 ) ∪ ( 0 , ∞ ) ( − ∞ , 0 ) ∪ ( 0 , ∞ )
( f g ) ( x ) = x + 2 , ( f g ) ( x ) = x + 2 , domain: ( − ∞ , 0 ) ∪ ( 0 , ∞ ) ( − ∞ , 0 ) ∪ ( 0 , ∞ )
( f g ) ( x ) = 4 x 3 + 8 x 2 , ( f g ) ( x ) = 4 x 3 + 8 x 2 , domain: ( − ∞ , 0 ) ∪ ( 0 , ∞ ) ( − ∞ , 0 ) ∪ ( 0 , ∞ )
( f + g ) ( x ) = 3 x 2 + x − 5 , ( f + g ) ( x ) = 3 x 2 + x − 5 , domain: [ 5 , ∞ ) [ 5 , ∞ )
( f − g ) ( x ) = 3 x 2 − x − 5 , ( f − g ) ( x ) = 3 x 2 − x − 5 , domain: [ 5 , ∞ ) [ 5 , ∞ )
( f g ) ( x ) = 3 x 2 x − 5 , ( f g ) ( x ) = 3 x 2 x − 5 , domain: [ 5 , ∞ ) [ 5 , ∞ )
( f g ) ( x ) = 3 x 2 x − 5 , ( f g ) ( x ) = 3 x 2 x − 5 , domain: ( 5 , ∞ ) ( 5 , ∞ )
- ⓑ f ( g ( x ) ) = 2 ( 3 x − 5 ) 2 + 1 f ( g ( x ) ) = 2 ( 3 x − 5 ) 2 + 1
- ⓒ f ( g ( x ) ) = 6 x 2 − 2 f ( g ( x ) ) = 6 x 2 − 2
- ⓓ ( g ∘ g ) ( x ) = 3 ( 3 x − 5 ) − 5 = 9 x − 20 ( g ∘ g ) ( x ) = 3 ( 3 x − 5 ) − 5 = 9 x − 20
- ⓔ ( f ∘ f ) ( − 2 ) = 163 ( f ∘ f ) ( − 2 ) = 163
f ( g ( x ) ) = x 2 + 3 + 2 , g ( f ( x ) ) = x + 4 x + 7 f ( g ( x ) ) = x 2 + 3 + 2 , g ( f ( x ) ) = x + 4 x + 7
f ( g ( x ) ) = x + 1 x 3 3 = x + 1 3 x , g ( f ( x ) ) = x 3 + 1 x f ( g ( x ) ) = x + 1 x 3 3 = x + 1 3 x , g ( f ( x ) ) = x 3 + 1 x
( f ∘ g ) ( x ) = 1 2 x + 4 − 4 = x 2 , ( g ∘ f ) ( x ) = 2 x − 4 ( f ∘ g ) ( x ) = 1 2 x + 4 − 4 = x 2 , ( g ∘ f ) ( x ) = 2 x − 4
f ( g ( h ( x ) ) ) = ( 1 x + 3 ) 2 + 1 f ( g ( h ( x ) ) ) = ( 1 x + 3 ) 2 + 1
- ⓐ ( g ∘ f ) ( x ) = − 3 2 − 4 x ( g ∘ f ) ( x ) = − 3 2 − 4 x
- ⓑ ( − ∞ , 1 2 ) ( − ∞ , 1 2 )
- ⓐ ( 0 , 2 ) ∪ ( 2 , ∞ ) ; ( 0 , 2 ) ∪ ( 2 , ∞ ) ;
- ⓑ ( − ∞ , − 2 ) ∪ ( 2 , ∞ ) ; ( − ∞ , − 2 ) ∪ ( 2 , ∞ ) ;
- ⓒ ( 0 , ∞ ) ( 0 , ∞ )
( 1 , ∞ ) ( 1 , ∞ )
sample: f ( x ) = x 3 g ( x ) = x − 5 f ( x ) = x 3 g ( x ) = x − 5
sample: f ( x ) = 4 x g ( x ) = ( x + 2 ) 2 f ( x ) = 4 x g ( x ) = ( x + 2 ) 2
sample: f ( x ) = x 3 g ( x ) = 1 2 x − 3 f ( x ) = x 3 g ( x ) = 1 2 x − 3
sample: f ( x ) = x 4 g ( x ) = 3 x − 2 x + 5 f ( x ) = x 4 g ( x ) = 3 x − 2 x + 5
sample: f ( x ) = x g ( x ) = 2 x + 6 f ( x ) = x g ( x ) = 2 x + 6
sample: f ( x ) = x 3 g ( x ) = ( x − 1 ) f ( x ) = x 3 g ( x ) = ( x − 1 )
sample: f ( x ) = x 3 g ( x ) = 1 x − 2 f ( x ) = x 3 g ( x ) = 1 x − 2
sample: f ( x ) = x g ( x ) = 2 x − 1 3 x + 4 f ( x ) = x g ( x ) = 2 x − 1 3 x + 4
f ( g ( 0 ) ) = 27 , g ( f ( 0 ) ) = − 94 f ( g ( 0 ) ) = 27 , g ( f ( 0 ) ) = − 94
f ( g ( 0 ) ) = 1 5 , g ( f ( 0 ) ) = 5 f ( g ( 0 ) ) = 1 5 , g ( f ( 0 ) ) = 5
18 x 2 + 60 x + 51 18 x 2 + 60 x + 51
g ∘ g ( x ) = 9 x + 20 g ∘ g ( x ) = 9 x + 20
( f ∘ g ) ( 6 ) = 6 ( f ∘ g ) ( 6 ) = 6 ; ( g ∘ f ) ( 6 ) = 6 ( g ∘ f ) ( 6 ) = 6
( f ∘ g ) ( 11 ) = 11 , ( g ∘ f ) ( 11 ) = 11 ( f ∘ g ) ( 11 ) = 11 , ( g ∘ f ) ( 11 ) = 11
A ( t ) = π ( 25 t + 2 ) 2 A ( t ) = π ( 25 t + 2 ) 2 and A ( 2 ) = π ( 25 4 ) 2 = 2500 π A ( 2 ) = π ( 25 4 ) 2 = 2500 π square inches
A ( 5 ) = π ( 2 ( 5 ) + 1 ) 2 = 121 π A ( 5 ) = π ( 2 ( 5 ) + 1 ) 2 = 121 π square units
- ⓐ N ( T ( t ) ) = 23 ( 5 t + 1.5 ) 2 − 56 ( 5 t + 1.5 ) + 1 N ( T ( t ) ) = 23 ( 5 t + 1.5 ) 2 − 56 ( 5 t + 1.5 ) + 1
- ⓑ 3.38 hours

3.5 Section Exercises
A horizontal shift results when a constant is added to or subtracted from the input. A vertical shifts results when a constant is added to or subtracted from the output.
A horizontal compression results when a constant greater than 1 is multiplied by the input. A vertical compression results when a constant between 0 and 1 is multiplied by the output.
For a function f , f , substitute ( − x ) ( − x ) for ( x ) ( x ) in f ( x ) . f ( x ) . Simplify. If the resulting function is the same as the original function, f ( − x ) = f ( x ) , f ( − x ) = f ( x ) , then the function is even. If the resulting function is the opposite of the original function, f ( − x ) = − f ( x ) , f ( − x ) = − f ( x ) , then the original function is odd. If the function is not the same or the opposite, then the function is neither odd nor even.
g ( x ) = | x - 1 | − 3 g ( x ) = | x - 1 | − 3
g ( x ) = 1 ( x + 4 ) 2 + 2 g ( x ) = 1 ( x + 4 ) 2 + 2
The graph of f ( x + 43 ) f ( x + 43 ) is a horizontal shift to the left 43 units of the graph of f . f .
The graph of f ( x - 4 ) f ( x - 4 ) is a horizontal shift to the right 4 units of the graph of f . f .
The graph of f ( x ) + 8 f ( x ) + 8 is a vertical shift up 8 units of the graph of f . f .
The graph of f ( x ) − 7 f ( x ) − 7 is a vertical shift down 7 units of the graph of f . f .
The graph of f ( x + 4 ) − 1 f ( x + 4 ) − 1 is a horizontal shift to the left 4 units and a vertical shift down 1 unit of the graph of f . f .
decreasing on ( − ∞ , − 3 ) ( − ∞ , − 3 ) and increasing on ( − 3 , ∞ ) ( − 3 , ∞ )
decreasing on ( 0 , ∞ ) ( 0 , ∞ )
g ( x ) = f ( x - 1 ) , h ( x ) = f ( x ) + 1 g ( x ) = f ( x - 1 ) , h ( x ) = f ( x ) + 1
f ( x ) = | x - 3 | − 2 f ( x ) = | x - 3 | − 2
f ( x ) = x + 3 − 1 f ( x ) = x + 3 − 1
f ( x ) = ( x - 2 ) 2 f ( x ) = ( x - 2 ) 2
f ( x ) = | x + 3 | − 2 f ( x ) = | x + 3 | − 2
f ( x ) = − x f ( x ) = − x
f ( x ) = − ( x + 1 ) 2 + 2 f ( x ) = − ( x + 1 ) 2 + 2
f ( x ) = − x + 1 f ( x ) = − x + 1
The graph of g g is a vertical reflection (across the x x -axis) of the graph of f . f .
The graph of g g is a vertical stretch by a factor of 4 of the graph of f . f .
The graph of g g is a horizontal compression by a factor of 1 5 1 5 of the graph of f . f .
The graph of g g is a horizontal stretch by a factor of 3 of the graph of f . f .
The graph of g g is a horizontal reflection across the y y -axis and a vertical stretch by a factor of 3 of the graph of f . f .
g ( x ) = | − 4 x | g ( x ) = | − 4 x |
g ( x ) = 1 3 ( x + 2 ) 2 − 3 g ( x ) = 1 3 ( x + 2 ) 2 − 3
g ( x ) = 1 2 ( x - 5 ) 2 + 1 g ( x ) = 1 2 ( x - 5 ) 2 + 1
The graph of the function f ( x ) = x 2 f ( x ) = x 2 is shifted to the left 1 unit, stretched vertically by a factor of 4, and shifted down 5 units.
The graph of f ( x ) = | x | f ( x ) = | x | is stretched vertically by a factor of 2, shifted horizontally 4 units to the right, reflected across the horizontal axis, and then shifted vertically 3 units up.
The graph of the function f ( x ) = x 3 f ( x ) = x 3 is compressed vertically by a factor of 1 2 . 1 2 .
The graph of the function is stretched horizontally by a factor of 3 and then shifted vertically downward by 3 units.
The graph of f ( x ) = x f ( x ) = x is shifted right 4 units and then reflected across the vertical line x = 4. x = 4.
3.6 Section Exercises
Isolate the absolute value term so that the equation is of the form | A | = B . | A | = B . Form one equation by setting the expression inside the absolute value symbol, A , A , equal to the expression on the other side of the equation, B . B . Form a second equation by setting A A equal to the opposite of the expression on the other side of the equation, − B . − B . Solve each equation for the variable.
The graph of the absolute value function does not cross the x x -axis, so the graph is either completely above or completely below the x x -axis.
The distance from x to 8 can be represented using the absolute value statement: ∣ x − 8 ∣ = 4.
∣ x − 10 ∣ ≥ 15
There are no x-intercepts.
(−4, 0) and (2, 0)
( 0 , − 4 ) , ( 4 , 0 ) , ( − 2 , 0 ) ( 0 , − 4 ) , ( 4 , 0 ) , ( − 2 , 0 )
( 0 , 7 ) , ( 25 , 0 ) , ( − 7 , 0 ) ( 0 , 7 ) , ( 25 , 0 ) , ( − 7 , 0 )
range: [ – 400 , 100 ] [ – 400 , 100 ]
There is no solution for a a that will keep the function from having a y y -intercept. The absolute value function always crosses the y y -intercept when x = 0. x = 0.
| p − 0.08 | ≤ 0.015 | p − 0.08 | ≤ 0.015
| x − 5.0 | ≤ 0.01 | x − 5.0 | ≤ 0.01
3.7 Section Exercises
Each output of a function must have exactly one output for the function to be one-to-one. If any horizontal line crosses the graph of a function more than once, that means that y y -values repeat and the function is not one-to-one. If no horizontal line crosses the graph of the function more than once, then no y y -values repeat and the function is one-to-one.
Yes. For example, f ( x ) = 1 x f ( x ) = 1 x is its own inverse.
Given a function y = f ( x ) , y = f ( x ) , solve for x x in terms of y . y . Interchange the x x and y . y . Solve the new equation for y . y . The expression for y y is the inverse, y = f − 1 ( x ) . y = f − 1 ( x ) .
f − 1 ( x ) = x − 3 f − 1 ( x ) = x − 3
f − 1 ( x ) = 2 − x f − 1 ( x ) = 2 − x
f − 1 ( x ) = − 2 x x − 1 f − 1 ( x ) = − 2 x x − 1
domain of f ( x ) : [ − 7 , ∞ ) ; f − 1 ( x ) = x − 7 f ( x ) : [ − 7 , ∞ ) ; f − 1 ( x ) = x − 7
domain of f ( x ) : [ 0 , ∞ ) ; f − 1 ( x ) = x + 5 f ( x ) : [ 0 , ∞ ) ; f − 1 ( x ) = x + 5
a. f ( g ( x ) ) = x f ( g ( x ) ) = x and g ( f ( x ) ) = x . g ( f ( x ) ) = x . b. This tells us that f f and g g are inverse functions
f ( g ( x ) ) = x , g ( f ( x ) ) = x f ( g ( x ) ) = x , g ( f ( x ) ) = x
not one-to-one
[ 2 , 10 ] [ 2 , 10 ]
| 1 | 4 | 7 | 12 | 16 | |
| 3 | 6 | 9 | 13 | 14 |
f − 1 ( x ) = ( 1 + x ) 1 / 3 f − 1 ( x ) = ( 1 + x ) 1 / 3
f − 1 ( x ) = 5 9 ( x − 32 ) . f − 1 ( x ) = 5 9 ( x − 32 ) . Given the Fahrenheit temperature, x , x , this formula allows you to calculate the Celsius temperature.
t ( d ) = d 50 , t ( d ) = d 50 , t ( 180 ) = 180 50 . t ( 180 ) = 180 50 . The time for the car to travel 180 miles is 3.6 hours.
Review Exercises
f ( − 3 ) = − 27 ; f ( − 3 ) = − 27 ; f ( 2 ) = − 2 ; f ( 2 ) = − 2 ; f ( − a ) = − 2 a 2 − 3 a ; f ( − a ) = − 2 a 2 − 3 a ; − f ( a ) = 2 a 2 − 3 a ; − f ( a ) = 2 a 2 − 3 a ; f ( a + h ) = − 2 a 2 + 3 a − 4 a h + 3 h − 2 h 2 f ( a + h ) = − 2 a 2 + 3 a − 4 a h + 3 h − 2 h 2
x = − 1.8 x = − 1.8 or or x = 1.8 or x = 1.8
− 64 + 80 a − 16 a 2 − 1 + a = − 16 a + 64 − 64 + 80 a − 16 a 2 − 1 + a = − 16 a + 64
( − ∞ , − 2 ) ∪ ( − 2 , 6 ) ∪ ( 6 , ∞ ) ( − ∞ , − 2 ) ∪ ( − 2 , 6 ) ∪ ( 6 , ∞ )
increasing ( 2 , ∞ ) ; ( 2 , ∞ ) ; decreasing ( − ∞ , 2 ) ( − ∞ , 2 )
increasing ( − 3 , 1 ) ; ( − 3 , 1 ) ; constant ( − ∞ , − 3 ) ∪ ( 1 , ∞ ) ( − ∞ , − 3 ) ∪ ( 1 , ∞ )
local minimum ( − 2 , − 3 ) ; ( − 2 , − 3 ) ; local maximum ( 1 , 3 ) ( 1 , 3 )
( − 1.8 , 10 ) ( − 1.8 , 10 )
( f ∘ g ) ( x ) = 17 − 18 x ; ( g ∘ f ) ( x ) = − 7 − 18 x ( f ∘ g ) ( x ) = 17 − 18 x ; ( g ∘ f ) ( x ) = − 7 − 18 x
( f ∘ g ) ( x ) = 1 x + 2 ; ( g ∘ f ) ( x ) = 1 x + 2 ( f ∘ g ) ( x ) = 1 x + 2 ; ( g ∘ f ) ( x ) = 1 x + 2
( f ∘ g ) ( x ) = 1 + x 1 + 4 x , x ≠ 0 , x ≠ − 1 4 ( f ∘ g ) ( x ) = 1 + x 1 + 4 x , x ≠ 0 , x ≠ − 1 4
( f ∘ g ) ( x ) = 1 x , x > 0 ( f ∘ g ) ( x ) = 1 x , x > 0
sample: g ( x ) = 2 x − 1 3 x + 4 ; f ( x ) = x g ( x ) = 2 x − 1 3 x + 4 ; f ( x ) = x
f ( x ) = | x − 3 | f ( x ) = | x − 3 |
f ( x ) = 1 2 | x + 2 | + 1 f ( x ) = 1 2 | x + 2 | + 1
f ( x ) = − 3 | x − 3 | + 3 f ( x ) = − 3 | x − 3 | + 3
f − 1 ( x ) = x - 9 10 f − 1 ( x ) = x - 9 10
f − 1 ( x ) = x - 1 f − 1 ( x ) = x - 1
The function is one-to-one.
Practice Test
The relation is a function.
The graph is a parabola and the graph fails the horizontal line test.
2 a 2 − a 2 a 2 − a
− 2 ( a + b ) + 1 − 2 ( a + b ) + 1
f − 1 ( x ) = x + 5 3 f − 1 ( x ) = x + 5 3
( − ∞ , − 1.1 ) and ( 1.1 , ∞ ) ( − ∞ , − 1.1 ) and ( 1.1 , ∞ )
( 1.1 , − 0.9 ) ( 1.1 , − 0.9 )
f ( 2 ) = 2 f ( 2 ) = 2
f ( x ) = { | x | if x ≤ 2 3 if x > 2 f ( x ) = { | x | if x ≤ 2 3 if x > 2
x = 2 x = 2
f − 1 ( x ) = − x − 11 2 f − 1 ( x ) = − x − 11 2
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.
Access for free at https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites
- Authors: Jay Abramson
- Publisher/website: OpenStax
- Book title: College Algebra
- Publication date: Feb 13, 2015
- Location: Houston, Texas
- Book URL: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites
- Section URL: https://openstax.org/books/college-algebra/pages/chapter-3
© Dec 8, 2021 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.
- $ 0.00 0 items
Unit 6 – Quadratic Functions and Their Algebra
Quadratic Function Review
LESSON/HOMEWORK
LESSON VIDEO
EDITABLE LESSON
EDITABLE KEY
Factoring Trinomials
Complete Factoring
Factoring by Grouping
The Zero Product Law
Quadratic Inequalities in One Variable
Completing the Square and Shifting Parabolas
Modeling with Quadratic Functions
Equations of Circles
The Locus Definition of a Parabola
Unit Review
Unit 6 Review – Quadratic Functions
UNIT REVIEW
EDITABLE REVIEW
Unit 6 Assessment Form A
EDITABLE ASSESSMENT
Unit 6 Assessment Form B
Unit 6 Assessment Form C
Unit 6 Assessment Form D
Unit 6 Exit Tickets
Unit 6 – Mid-Unit Quiz (Through Lesson #6) – Form A
Unit 6 – Mid-Unit Quiz (Through Lesson #6) – Form B
Unit 6 – Mid-Unit Quiz (Through Lesson #6) – Form C
Unit 6 – Mid-Unit Quiz (Through Lesson #6) – Form D
U06.AO.01 – Lesson 5.4 – Factoring Trinomials Using the AC Method
EDITABLE RESOURCE
U06.AO.02 – Lesson 5.5 – Using Structure to Factor
U06.AO.03 – Lesson 9.5 – The Vertex Form of a Parabola
U06.AO.04 – Lesson 12 – More Work with the Directrix and Focus
U06.AO.05 – Parabola Practice
U06.AO.06 – Factoring Practice
U06.AO.07 – Quadratic Systems Practice
U06.AO.08 – Quadratic Inequalities in One Variable Practice
Thank you for using eMATHinstruction materials. In order to continue to provide high quality mathematics resources to you and your students we respectfully request that you do not post this or any of our files on any website. Doing so is a violation of copyright. Using these materials implies you agree to our terms and conditions and single user license agreement .
The content you are trying to access requires a membership . If you already have a plan, please login. If you need to purchase a membership we offer yearly memberships for tutors and teachers and special bulk discounts for schools.
Sorry, the content you are trying to access requires verification that you are a mathematics teacher. Please click the link below to submit your verification request.

Home > CC3 > Chapter 7 > Lesson 7.3.3
Lesson 7.1.1, lesson 7.1.2, lesson 7.1.3, lesson 7.2.1, lesson 7.2.2, lesson 7.2.3, lesson 7.2.4, lesson 7.2.5, lesson 7.3.1, lesson 7.3.2, lesson 7.3.3.
© 2022 CPM Educational Program. All rights reserved.
- Texas Go Math
- Big Ideas Math
- Engageny Math
- McGraw Hill My Math
- enVision Math
- 180 Days of Math
- Math in Focus Answer Key
- Math Expressions Answer Key
- Privacy Policy
Eureka Math Grade 3 Module 3 Lesson 11 Answer Key
Teachers and students can find this Eureka Book Answer Key for Grade 3 more helpful in raising students’ scores and supporting teachers to educate the students. Learning activities are the best option to educate elementary school kids and make them understand the basic mathematical concepts like addition, subtraction, multiplication, division, etc. Grade 3 elementary school students can find these fun-learning exercises for all math concepts through the Eureka Book.
Engage NY Eureka Math 3rd Grade Module 3 Lesson 11 Answer Key
Students of Grade 3 can get a strong foundation by referring to the Eureka Math Book. It was developed by highly professional mathematics educators and the solutions prepared by them are in a concise manner for easy grasping. To achieve high scores in Grade 3, students need to solve all questions and exercises included in Eureka Grade 3 Book.
Eureka Math Grade 3 Module 3 Lesson 11 Pattern Sheet Answer Key
Eureka Math Grade 3 Module 3 Lesson 11 Problem Set Answer Key
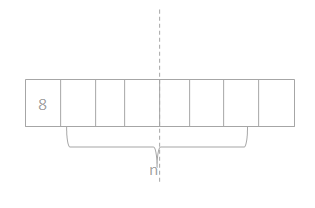
Question 1. Ms. Santor divides 32 students into 8 equal groups for a field trip. Draw a tape diagram, and label the number of students in each group as n. Write an equation, and solve for n.
Answer: 32 / n = 8. n = 4.
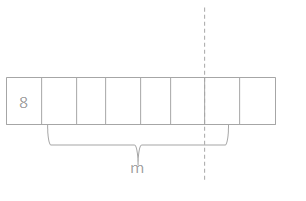
Question 2. Tara buys 6 packs of printer paper. Each pack of paper costs $8. Draw a tape diagram, and label the total amount she spends as m. Write an equation, and solve for m.
Answer: The total amount she spends = $48.
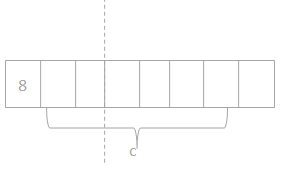
Answer: The total amount of coffee beans he buys = 3 kg.
Question 4. Eight boys equally share 4 packs of baseball cards. Each pack contains 10 cards. How many cards does each boy get?
Answer: The number of cards each boy gets = 40.
Explanation: In the above-given question, given that, Eight boys equally share 4 packs of baseball cards. each pack contains 10 cards. 10 x 4 = 40. so the number of cards each boy gets = 40.
Question 5. There are 8 bags of yellow and green balloons. Each bag contains 7 balloons. If there are 35 yellow balloons, how many green balloons are there?
Answer: The number of green balloons = 21.
Explanation: In the above-given question, given that, There are 8 bags of yellow and green balloons. each bag contains 7 balloons. if there are 35 yellow balloons. 8 x 7 = 56. 56 – 35 = 21. so the number of green balloons = 21.
Question 6. The fruit seller packs 72 oranges into bags of 8 each. He sells all the oranges at $4 a bag. How much money did he receive?
Answer: The amount of money he receives = 40.
Explanation: In the above-given question, given that, The fruit seller packs 72 oranges into bags of 8 each. He sells all the oranges at $4 a bag. 8 x 4 = 32. 72 – 32 = 40. so the amount of money he receives = 40.
Eureka Math Grade 3 Module 3 Lesson 11 Exit Ticket Answer Key
Erica buys some packs of rubber bracelets. There are 8 bracelets in each pack.
a. How many packs of rubber bracelets does she buy if she has a total of 56 bracelets? Draw a tape diagram, and label the total number of packages as p. Write an equation, and solve for p.
Answer: The total amount of packages = 7.
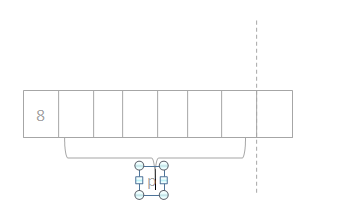
b. After giving some bracelets away, Erica has 18 left. How many bracelets did she give away?
Answer: The number of bracelets did she give away = 9.
Explanation: In the above-given question, given that, After giving some bracelets away, Erica has 18 left. 18 / 2 = 9. so the number of bracelets did she give away = 9.
Eureka Math Grade 3 Module 3 Lesson 11 Homework Answer Key
Question 1. Jenny bakes 10 cookies. She puts 7 chocolate chips on each cookie. Draw a tape diagram, and label the total amount of chocolate chips as c. Write an equation, and solve for c.
Answer: The total amount of chocolate chips = 70.
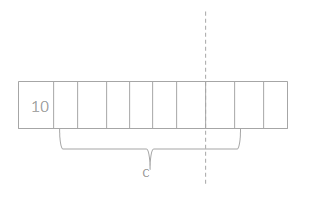
Question 2. Mr. Lopez arranges 48 dry erase markers into 8 equal groups for his math stations. Draw a tape diagram, and label the number of dry erase markers in each group as v. Write an equation, and solve for v.
Answer: The number of dry erase markers in each group = 6.
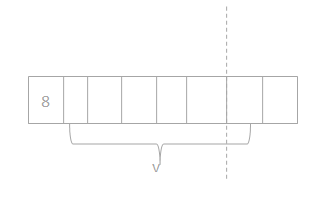
Question 3. There are 35 computers in the lab. Five students each turn off an equal number of computers. How many computers does each student turn off? Label the unknown as m, and then solve.
Answer: The number of computers does each student turn off = 7.
Question 4. There are 9 bins of books. Each bin has 6 comic books. How many comic books are there altogether?
Answer: The number of comic books is there altogether = 54.
Explanation: In the above-given question, given that, There are 9 bins of books. Each bin has 6 comic books. 9 x 6 = 54. so the number of comic books is there altogether = 54.
Question 5. There are 8 trail mix bags in one box. Clarissa buys 5 boxes. She gives an equal number of bags of trail mix to 4 friends. How many bags of trail mix does each friend receive?
Answer: The bags of trail mix does each friend receives = 40.
Explanation: In the above-given question. given that, There are 8 trail mix bags in one box. Clarissa buys 5 boxes. she gives an equal number of bags of trail mix to 4 friends. 8 x 5 = 40.
Question 6. Leo earns $8 each week for doing chores. After 7 weeks, he buys a gift and has $38 left. How much money does he spend on the gift?
Answer: The amount he spends on the gift = $18.
Explanation: In the above-given question, given that, Leo earns $8 each week for doing chores. After 7 weeks, he buys a gift and has $38 left. 7 x 8 = 56. 56 – 38 = $18. so the amount he spends on the gift = $18.
Leave a Comment Cancel Reply
You must be logged in to post a comment.

IMAGES
VIDEO
COMMENTS
Eureka Math Grade 3 Module 3 Lesson 10 Problem Set Answer Key. Question 1. Label the arrays. Then, fill in the blanks below to make the statements true. 8 x 8 = 64. the number of rows = 8. the number of columns = 8. 8 x 8 = 8 x ( 5 + 3 ). 40 + 24.
Here is a link to the source for the pages, the "full module" PDF:https://www.engageny.org/resource/grade-3-mathematics-module-3
NYS COMMON CORE MATHEMATICS CURRICULUM 3•Lesson 3 Answer Key Lesson 3 Problem Set 1. e = 20; l = 7; i = 6; c = 3; s = 4; n= 10; t = 70; k = 9; b = 2; a = 24; h = 5; kitchen tables 2. a. m = $24 b. c = $6 3. 4, n, 28; 28, 4, n; n = 7; 7 pans 4. Shorter game: 10 minutes; longer game: 22 min Exit Ticket 1. 45 2. 5 3. 3 4. 28 5.
So, teachers, parents, and students can trust the Eureka Math Answer Keys for all grades and start their preparation. Utilize these handy resources ie., Eureka Math Grade 3 Solution key Pdf & become pro in math. Simply hit on the required module link and prepare the topics covered in it thoroughly and also clarify your queries about the subject.
The source for the homework pages is the full module PDF, available for free here:https://www.engageny.org/resource/grade-3-mathematics-module-4
CPM Educational Program - solutions and answers
6. Draw an array using factors 2 and 3. Then, show a number bond where each part represents the amount in one row. X X X X X X X X X X X X. A STORY OF UNITS. 11. ©2015 Great Minds. eureka-math.org. Lesson 3 Homework 3•1. Lesson 3: Interpret the meaning of factors—the size of the group or the number of groups.
Answer Key Lesson 3.3 Practice Level A 1. yes; Corresponding Angles Converse 2. yes; Alternate Interior Angles Converse 3. yes; Alternate Exterior Angles Converse 4. yes; Corresponding Angles Converse 5. no 6. yes; Alternate Interior Angles Converse 7. 40 8. 30 9. 30 10. 14 11. 32 12. 95 13. C 14. m i n 15. p i q 16. p i q 17. neither 18. Given; Corresponding Angles Postulate; Given ...
Order the distances from least to greatest. 62.95 meters, 63.37 meters, 63.7 meters Chapter 3 P57. Lesson Check (CC.5.NBT.3b) Jay, Alana, Evan, and Stacey work together to complete a science experiment. The table at the right shows the amount of liquid left in each of their beakers at the end of the experiment. 1.
Core Connections Geometry - 2nd Edition - Solutions and ...
Eureka Math Grade 3 Module 3 Lesson 19 Problem Set Answer Key. Question 1. Use the disks to fill in the blanks in the equations. a. 4 x 3 = 12. the number of rows = 4. the number of columns = 3. 4 x 3 ones = 12 ones. 4 x 3 = 12.
Common Core Algebra II
1. Find the numbers that make the function in the denominator g g equal to zero, and check for any other domain restrictions on f f and g, g, such as an even-indexed root or zeros in the denominator. 3. Yes. Sample answer: Let f (x) = x + 1 and g (x) = x − 1. f (x) = x + 1 and g (x) = x − 1.
3.10 Trig Equations and Inequalities
Exercise 86. Exercise 87. Exercise 88. Exercise 89. Exercise 90. Exercise 91. Find step-by-step solutions and answers to College Algebra - 9780321729682, as well as thousands of textbooks so you can move forward with confidence.
Eureka Math Grade 3 Module 3 Lesson 21 Homework Answer Key. Use the RDW process for each problem. Use a letter to represent the unknown. Question 1. ... Eureka Math Grade 3 Module 3 Lesson 21 Template Answer Key. Answer: 30 x 6 = 180, 9 x 60 = 540, 40 x 2 = 80, 10 x 6 = 60, 70 x 3 = 210, 50 x 6 = 300, 80 x 9 = 720, 20 x 5 = 100, 8 x 30 = 240, 3 ...
Exercise 57. Exercise 58. Exercise 59. Exercise 60. Exercise 61. Exercise 62. Find step-by-step solutions and answers to College Algebra - 9780134217451, as well as thousands of textbooks so you can move forward with confidence.
Assessment. Unit 6 - Mid-Unit Quiz (Through Lesson #6) - Form D. ASSESSMENT. ANSWER KEY. EDITABLE ASSESSMENT. EDITABLE KEY.
Engage NY Eureka Math 3rd Grade Module 3 Lesson 12 Answer Key. ... Eureka Math Grade 3 Module 3 Lesson 12 Homework Answer Key. Question 1. Find the value of each row. Then, add the rows to find the total. a. Each has a value of 6. 9 × 6 = ___54_____ 9 × 6 = (5 + 4) × 6
utes.Grades 7-9: 3-5 assignments a week, each lasting 45-75 m. utes.Grades 10-12: 4-5 assignments a week, each lasting 75-120 m. utes.Many high school students, like these Kingwood High School football players in Houston, Texas, have obligations after school that limit their homewor.
CPM Education Program proudly works to offer more and better math education to more students.
Eureka Math Grade 3 Module 3 Lesson 9 Problem Set Answer Key. Question 1. Use the array to complete the equation. a. The number of rows = 3. the number of columns = 12. The number of rows = 3. the number of columns = 12.
Eureka Math Grade 3 Module 3 Lesson 11 Homework Answer Key. Question 1. Jenny bakes 10 cookies. She puts 7 chocolate chips on each cookie. Draw a tape diagram, and label the total amount of chocolate chips as c. Write an equation, and solve for c. Answer: The total amount of chocolate chips = 70. Explanation: